Limiting Chance is a series that uses mathematics and probability to investigate aspects of Limited play. In this article, I continue my investigation of mulligans.
Mulligan Rules
Let’s get this out of the way right from the start. Is it possible to calculate perfect mulligan rules using mathematics? No.
There is no such thing as perfect mulligan rules. It’s simply not possible to capture the subtlety of a mulligan decision with a set of instructions. There are too many elements that factor into the decision of whether to mulligan.
- The number of low-cost spells in my hand.
- Whether my lands match the color of those spells.
- How many of those spells are creatures.
- Whether those creatures can keep me alive if I stumble on land.
- How fast I think my deck is.
- How fast I think the environment is.
- How fast I think my opponent’s deck is.
Can all of those factors be accounted for in a simple set of mulligan rules? No. But there is one factor of primary importance that stands above the others:
- The number of lands in my hand.
I can use probability to calculate a set of guidelines that account only for that most important factor: the number of lands in my hand. Once I have those guidelines and it comes time to make a real-life mulligan decision, I can account for the other factors. I can decide for any particular hand whether I am going to abide by the guidelines or I am going to make an exception.
In this article, I calculate guidelines for when I am on the draw. I assume a 40-card deck with seventeen lands.
Competitive Start
To calculate mulligan rules, I need to define the goal of the rules. The goal, of course, is to give me a solid starting hand. A hand with enough spells that I won’t run out of gas early and enough lands that I won’t miss an early land drop. I will use the definition of a competitive start I put forth in my previous article. (If you have not read that article, I ask you to do so. In this article, I assume that concepts presented in the previous article are familiar to the reader.) I defined a competitive start in that article as when I have:
- Four or more lands by turn 4 and
- Four or more spells by turn 4
I will calculate a set of mulligan rules that maximizes my chances of achieving that competitive start on the draw.
Three Cards
The most straightforward way to do this calculation is to start at the smallest hand and work my way up. I’ll start with a three-card hand.
If I start the game with three cards, by turn 4 I will have seven cards. It takes a minimum of eight cards for a competitive start (four lands and four spells). So there is no three-card starting hand that gives me any chance of a competitive start. Across the board the chance of a competitive start with three cards is zero.
I must avoid mulling to a three-card hand. I doubt that’s news to you.
Four Cards
Four cards, unlike three cards, give me a greater-than-zero chance for a competitive start. That chance varies based on the number of lands in my hand. According to my Magic Probability Toolkit, these are the probabilities:

All of the four-card hands have a higher chance of getting me to a competitive start than any three-card hand. As such, I should keep any four-card hand that I draw.
I can calculate the overall chance of getting a competitive start from a four-card hand by multiplying each of the above probabilities by the chance of drawing that particular hand. Here are the results.
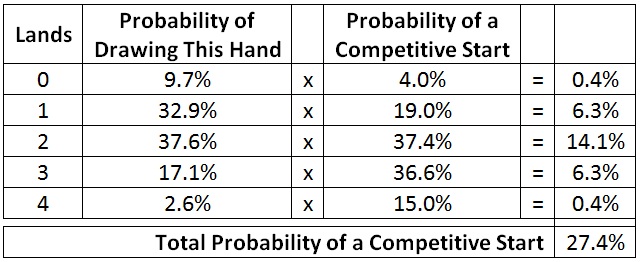
The overall chance of getting a competitive start with a four-card hand is a little over 25%. While those odds aren’t great, they’re higher than I would have guessed. I suppose the lesson here is that when I am looking at a bad five-card hand, I shouldn’t give up. I should mull to four and fight it out. There’s actually a one in four chance I’ll give my opponent a run for their money. Now, I’m not saying they won’t overwhelm me with card advantage later, but I need to fight for that small chance of victory. Being a good Magic player is all about eking out small advantages around the edges, and with a four-card hand I am definitely on the edge.
(Now for a quick probability geek side note. Did you notice that in the far right column of the table, the probabilities are symmetric? 0.4% is the first and last probability, 6.3% is the second and fourth probability. That is something that will only occur with four-card hands. Why did it happen? Because to get a competitive start from four cards, in the first four turns I have to draw exactly the opposite of my starting hand. For example, if my starting hand is four lands, I need to draw four spells. If my starting hand is three spells and one land, I need to draw one spell and three lands. That symmetry causes the probabilities to be symmetric. Ok, end of side note. Sorry about that. I couldn’t resist.)
Five Cards
Here are the chances the Magic Probability Toolkit gives for the various five-card hands.

Now for the key piece of logic in this analysis. Since my goal is to maximize my chance of a competitive start, I should mulligan any five-card hand that has a lower probability than the average four-card hand. From the previous section, I know a four-card hand has a 27.4% chance.
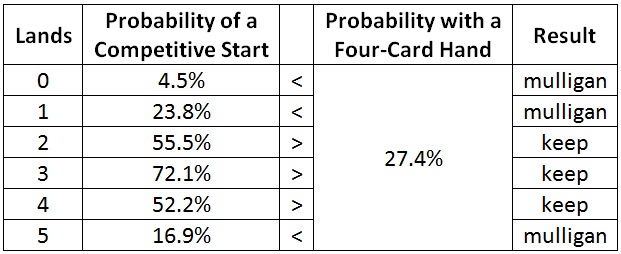
With five cards, I should mulligan hands that have zero, one, or five lands. I now have my guideline for five-card hands.
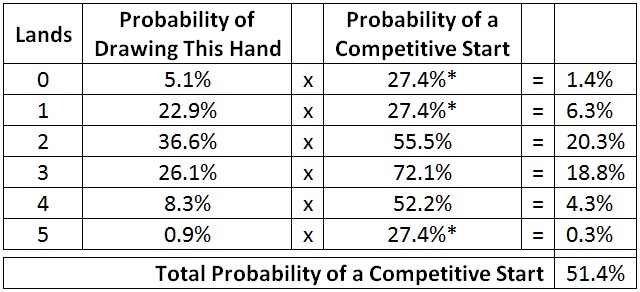
Before I move on to six cards, I first need to know the overall probability of a competitive start for a five-card hand. I can calculate that in the same way I did for a four-card hand with one difference. For zero-, one-, and five-land hands, in place of their actual probability of a competitive start, I need to substitute the average probability that a four-card hand gives. That’s because I know I am going to mulligan those hands. Those hands are effectively just four-card hands, so for them I need to use the average probability of a four-card hand.
I’ve put an asterisk (*) next to the cases where I’ve done that substitution. The effect of the substitution is a slight increase in the overall probability.
Six Cards
Six cards work the same as five cards. I won’t waste words; I’ll just show the numbers. Here is the probability of a competitive start for various six-card hands.
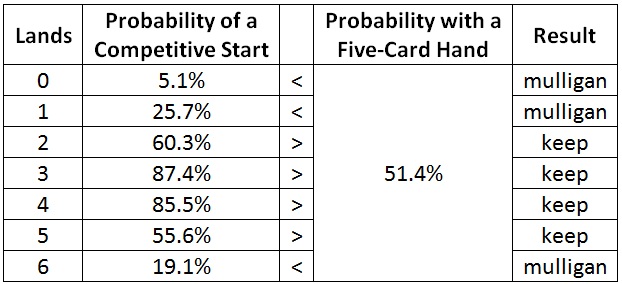
With six cards, I should mulligan hands that have zero, one, or six lands. I now have my six-card guideline.
Here is the overall probability of a competitive start with a six-card hand. Again, I’ve marked the substitutions with an asterisk (*).

Note that the overall probability calculated here of 71.0% for a six-card hand is higher than the 65.8% found in the previous article. In that article, I did not account for the increased probability gained by the option of mulliganing to five.
Seven Cards
Here is the probability of a competitive start for various seven-card hands.

The guideline for seven-card hands is to mulligan zero, one, two, six, and seven lands.
It’s worth noting that the two-land hand is the closest comparison. It’s thus no surprise that the two-land hand is the most contentious of mulligan decisions. It’s a decision that requires looking at other factors. Factors such as how many playable two- and three-drops my hand has and whether I think I can survive the extra time I’ll need to wait for my five- and six-drops. But it’s useful to know, all other things being equal, that the math favors a mulligan.
The Guidelines
Now I will bring the results together. The mulligan rules that maximize my chance of a competitive start when I am on the draw, using the definition of a competitive start I gave at the start of the article, are as follows:
- For seven-card hands, mulligan hands with less than three lands and more than five lands.
- For six-card hands, mulligan hands with less than two lands and more than five lands.
- For five-card hands, mulligan hands with less than two lands and more than four lands.
- Keep all four-card hands.
It’s also worth noting the cases when the probability comparison is close. Those are the times when I have the most leeway to factor in other considerations. The probability gap between mulling and keeping is within 10% for these hands:
- Two lands in a seven-card hand.
- Two and five lands in a six-card hand.
- One land in a five-card hand.
- Zero lands in a four-card hand.
Probability of Keeping
Given these mulligan rules, I can calculate the probability that I will keep my hand at each hand size. This gives me the chance that I will like the hand I’m about to mulligan to.
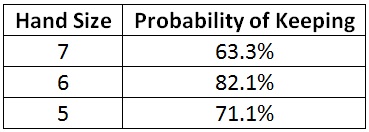
What do these numbers mean? 63% of the time I will keep my starting hand of seven. If I mulligan, the chance that I will like what I get and keep at six is 82%. That’s pretty high. If I’m required to mulligan again, the chance that I will like my five-card hand is 71%.
The Impact of Mulligans
One thing that excites me about having these mulligan guidelines is that they open the door to a new set of calculations. I am no longer forced to ignore the impact of mulligans, as I did in Limiting Chance: Gold Cards And Gatecreepers, or assume that all starting hands have three lands, as I did in Limiting Chance: Mana Development. While rote application of the guidelines does not model mulligans perfectly, it gives a reasonable approximation. The starting hand that results from applying these guidelines is much closer to the true starting hand that players experience during real games.
So, equipped with a mathematical model for mulligans, the first thing I’d like to do is see what mulligans do for me. How do they improve my starting hand and my early game?
Starting Land Count
What does my opening hand look like after mulligans? Here is the probability distribution of land counts in my opening hand before and after mulligans. The "Before Mulligans" column is taken straight from Limiting Chance: The Opening Hand.

Let’s take a close look at the probabilities. The chance of a six- or seven-land hand is eliminated entirely. That’s because the rules never keep those hands. Starting with zero lands is now very rare (one out of every 500 games played), and the chance of a one-land hand is extremely reduced. A two-land hand is still fairly common, but the probability is almost halved. The probability of those undesirable hands has shifted into three- and four-land hands. Their probability is higher. Five-land hands show almost no change.

Taken together, these probabilities show the average number of lands in my opening hand increasing by about a third of a land.
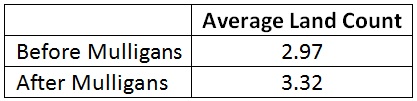
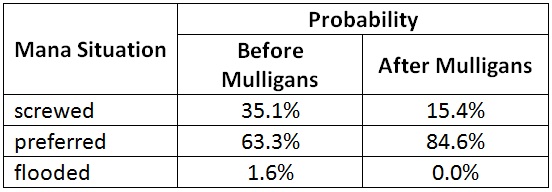
Using the same categories as my first article, I can see how much the chance of a preferred land count has improved.
Turn Cost
In Limiting Chance: Mana Development, I looked at the average turn on which various spells are first castable, a quantity I dubbed the spell’s turn cost. In that article, in order to do the calculation, I had to assume a three-land starting hand. Now I can calculate a more accurate turn cost, one that accounts for all starting hands with the appropriate probability after mulligans. Here are the turn costs for spells of several converted mana costs when on the draw.
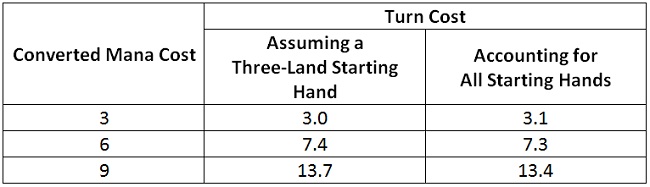
In general, I find that the turn cost of spells is lower than I previously calculated. That’s because the average number of lands in my starting hand is actually greater than three.
However, for low-cost spells, such as those with a converted mana cost of three, I find the turn cost to be higher. My previous assumption of a three-land starting hand meant I always had three mana on turn 3. Now I am correctly accounting for the chance that I won’t. That chance is small, but it still slightly increases the average casting turn.
Starting Hand Size
Here is an interesting quantity to look at. How do mulligans affect my starting hand size? I know they will make my average hand smaller, but by how much?

My average hand size drops by about half a card. Averaged across all games, half a card per game is the price I pay for to mulligan.
It is also interesting to look at the probability of each hand size after mulligans. Here are those probabilities.

What do these numbers tell me? In about one of every three games, I mulligan and then keep at six cards. 5% of the time, or one in every 20 games, I end up with five cards. In 2% of games, or one of every 50 games, I start with four cards.

Other Rules
These mulligan guidelines result in an 85% probability of a competitive start. Can I do better? Many people advocate keeping two-land hands; maybe I should. Perhaps I should mulligan five lands. If the calculation was performed correctly, other rules will give a lower probability. To check, I can change the rules and see what probability I get. Here are the probabilities for a competitive start with various tweaks to the mulligan rules for seven-card hands. The rules for five- and six-card hands are left unchanged.
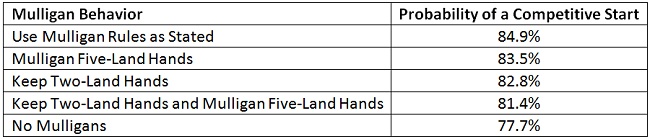
It’s no surprise, but the guidelines as stated result in the largest probability.
Of course, there can still be disagreement about the guidelines. In truth, however, it is more appropriate to direct disagreement towards the guidelines’ goals: the definition of a competitive start. For example, it has been suggested that the desire for four spells and four lands by turn 4 is too greedy. Perhaps I would be better served by a more modest goal, such as three spells and three lands by turn 3. Such a goal will result in different rules.
Further Work
In this article, I calculated guidelines for when I am on the draw. Correct mulligan advice when on the play may be different. I should calculate the guidelines for when I am on the play.
I should also look into the mulligan rules that come from other goals, other definitions of a competitive start. It would be good to know the rules that result from a more modest goal, such as three lands and three spells by turn 3. Or the rules that result from a goal more appropriate to an aggressive deck with a curve that tops out at four mana. A goal for such a deck might be three land and five spells by turn 4.
Finally, I am not accounting for color. I need to find a good way to account for land type and spell color in mulligan decisions. I need a definition for a competitive start that accounts for color, as well as a method for expressing the complex guidelines in a way that is understandable and easy to remember.
Takeaways
Here are the mulligan guidelines in a handy table. They apply to a seventeen-land, 40-card deck when you are on the draw. To use the table, mulligan hands with an ‘X‘.

This second table is more complex but also more useful. It indicates cases when the mulligan decision is close. When using this table, mulligan hands with an ‘X‘. For hands with a ‘?‘, consider a mulligan.

These are not meant to be hard and fast rules. Instead, they are the starting point for making your mulligan decision. Choose a table and commit it to memory.
[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit
