Limiting Chance is a series that uses mathematics and probability to investigate aspects of Limited play. In this article, I wrap up my look into mulligans, focusing on games when I am on the play. After deriving mulligan guidelines on the play, I use them to compare mana development between games on the play and games on the draw. Finally, I touch on alternate mulligan goals and derive the mulligan behavior to best reach them.

If you have not read my previous two articles, “Limiting Chance: A Competitive Start” and “Limiting Chance: Optimal Mulligans”, you should do so now. They explain in more detail several aspects of the investigation that in this article I assume you understand.

Throughout the article I use a 40-card deck with seventeen lands.

Mulligans on the Play

Experience has taught me to be more sensitive to mediocre opening hands when I’m on the play. When I’m going first, I get one less card to dig me out of a bad start. Take two-land hands for example. It’s very frightening to drop that first-turn land and be left with only one land in my hand.

But that’s a mix of emotion and intuition. To what degree am I actually more vulnerable to two-land hands on the play? For example, how much does being on the play change the probability of hitting my third land drop? In a previous article, I calculated the odds of getting my third land in time when I start with a two-land hand and I am on the draw. How does that compare to when I am on the play? Here is the probability of not hitting that land drop on the play and on the draw.

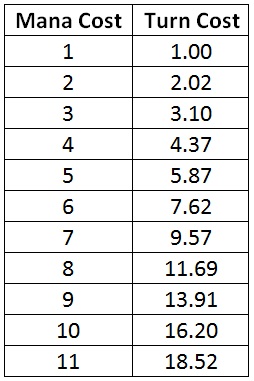
On the play, I miss my third land drop almost a third of the time. That’s twice as often as on the draw, a significant and noticeable increase.

What about the probability of getting my fourth land? I won’t be as greedy this time. Here is the probability of not hitting my fourth land drop by turn 5, again assuming I start with a two-land hand.

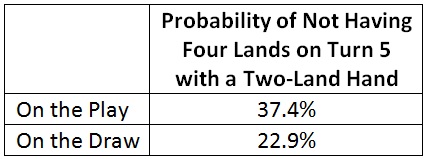
The probability is worse on the play. Not twice as bad this time, but still significantly worse.

The numbers clearly demonstrate that when I’m on the play, the stability of my early game is more sensitive to bad hands. On its own that indicates I should be more willing to mulligan. Yet when I’m on the play, I’m also more sensitive to the card disadvantage that comes with a mulligan. If I mulligan even once, I feel quite behind. During my opponent’s first turn, I’ve got only five cards in hand, while my opponent is holding a grip of seven. That makes me less eager to mulligan.

Accounting for both factors, I suspect that the correct mindset is to be more willing to mulligan on the play. The highest priority at the start of the game is a successfully early game: to get out some lands and start rolling. Card advantage becomes important in the mid to late game, but first things first. I need to survive the early game to get to the midgame. And entering the midgame on my heels is a surefire way to end up at an even greater card disadvantage.

Putting conjecture aside, let’s see what the math has to say.

Competitive Start

In this article, I will use the same definition of a competitive start that I have previously.

Four or more land by turn 4.
Four or more spells by turn 4.

Let’s look at my chance of obtaining a competitive start with the various seven-card starting hands, comparing games when I am on the play to those when I am on the draw.

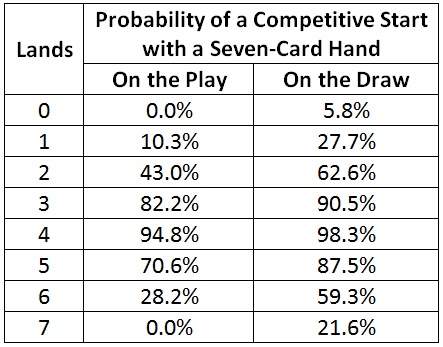
As expected, my chance of a competitive start is worse in all cases.

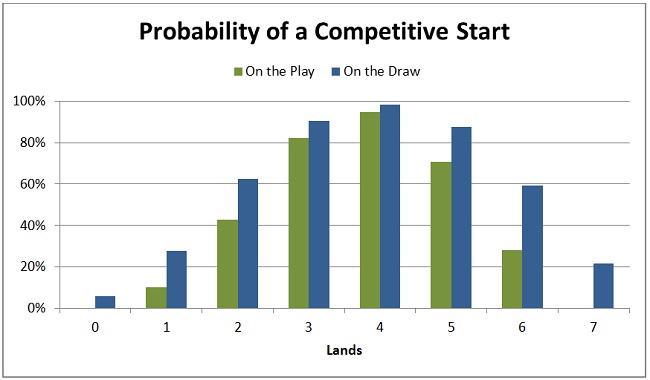
For good starting hands, such as three- and four-land hands, my chance drops only very slightly.

For starting hands that are already on the edge, such as two- and six-land hands, the chance of being competitive drops substantially. The chance with six lands drops by more than half. I have to draw three spells in a row to meet the criteria for being competitive.

Notice that for zero- and seven-land hands, the chance of being competitive has disappeared entirely. That’s because if I start with zero lands, it’s impossible to get to four lands by turn 4 because I only get three draws by turn 4. (We will see that this fact adds a wrinkle to the calculation and makes the process of constructing a mathematical model for mulligans on the play slightly more complex.)

Optimal Mulligans

Now I will calculate the mulligan behavior that maximizes my chance of having a competitive start on the play. It will be interesting to see how that behavior differs from the optimal mulligan guidelines on the draw, which I calculated in a previous article. As in that article, I start with smallest hand size and work my way up to a seven-card hand.

Four Cards

On the draw, a four-card hand has a greater-than-zero probability of a competitive start. On the play however, every four-card hand has no chance at all. That is because the criteria for a competitive start require eight cards on turn 4 and I cannot get to eight cards on turn 4 when I start with only four. When I’m on the play, I skip my first turn draw.

Presumably that means I should never mulligan to four. Let’s jump to five cards and give that a closer look.

Five Cards

Here are the probabilities of a competitive start for the various five-card hands.

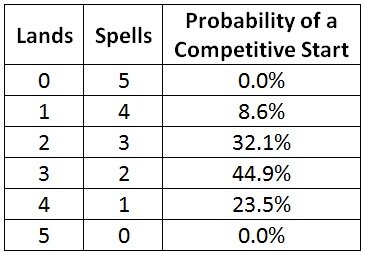
I should obviously keep hands with one through four lands. They have greater-than-zero probability of a competitive start, and that beats the 0% that any four-card hand gives.

What about zero- and five-land hands? As expected, those hands give no chance of a competitive start. It is not possible to draw four lands in three draws. The probability is tied with the average four-card hand. Should I mulligan or should I keep? The current system does not distinguish. It has no advice to give. I must add additional criteria to make the decision.

Secondary Criteria

I must introduce an additional rule to the analysis to break the tie. If I have no chance of getting four spells and four lands by turn 4, it seems reasonable to at least try to reach that goal by turn 5. I will use the probability of reaching the goal by turn 5 to break ties when a competitive start is impossible.

Let’s look at the chance of meeting the secondary criteria for three-, four-, and five-card hands. (Interestingly, these are the same probabilities as for a fourth-turn competitive start on the draw.)

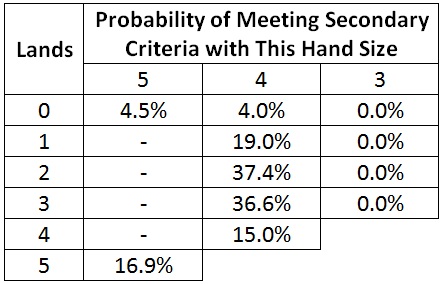
Three-land hands have no chance of meeting even the secondary criteria. I can conclusively say that I should never mull to three.

In order to determine which five-card hands I should mulligan, I need to calculate the average probability of meeting the secondary criteria with a four-card hand. If a particular five-card hand gives a worse probability, I should mulligan it.

Since I never mulligan a four-card hand, calculating the average chance of meeting the secondary criteria is straightforward. It’s the chance of meeting the criteria by just drawing eight cards: the first four in my starting hand and the second four during turns two through five. That probability is:

That probability is higher than the probability from a zero- or five-land five-card hand. So I should mulligan zero and five-land hands. I now have my guideline for five-card hands.

(Honestly, all this talk of tied probabilities and secondary criteria took more time than it was worth. But I want to be upfront with the reader about how my mulligan guidelines are calculated. I want the explanation to be thorough enough that others can repeat the process. Also, for the purpose of creating a mathematical model for mulligans, I need to know what to do even for these very unlikely, abysmal hands.)

Now that I have a mulligan guideline for five-card hands, I can calculate the average probability of a competitive start with a five-card hand. Because my rules have me mulliganing only zero-probability hands and because the resulting four-card hand also has zero probability, the mulligans do not affect the average probability. Thus the average probability is simple to calculate. It is the chance of having four lands and four spells with eight draws: five from the starting hand and three during turns 2 through 4. That’s obviously the same probability as above.

Six Cards

Here are the chances for a competitive start from the various six-card hands.

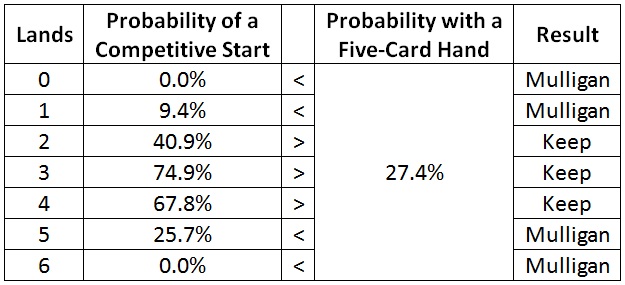
I want to mulligan any hand that gives a lower chance of a competitive start than the average five-card hand. The math says to mulligan two-, three-, and four-land hands. I now have my guideline for six-card hands.

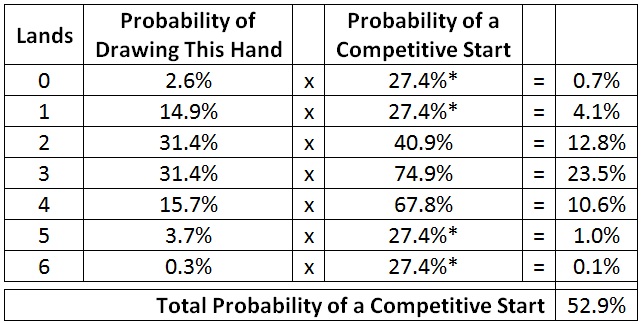
Here is the overall probably of a competitive start with six cards, using the substitution method for mulliganed hands detailed in the previous article.

Seven Cards

Finally, we come to seven-card hands.

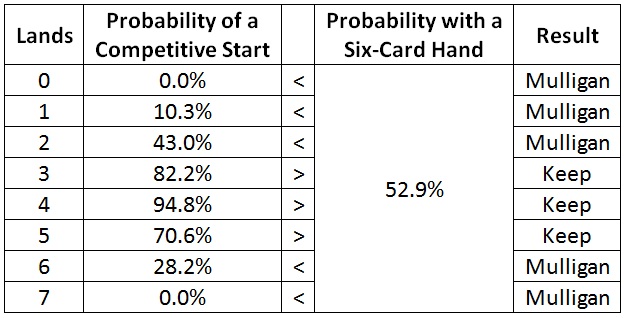
According to the math, I should keep three-, four-, and five-land hands and mulligan the rest.

Guidelines on the Play

Bringing the results together, I have the following mulligan guidelines on the play.

For seven-card hands, mulligan hands with less than three lands and more than five lands.
For six-card hands, mulligan hands with less than two lands and more than four lands.
For five-card hands, mulligan hands with less than one land and more than four lands.
Keep all four-card hands.

Using these guidelines maximizes my chance of a competitive start on the play, using the definition of a competitive start given earlier in the article.

It’s also worth noting the cases when the probability comparison is close. Those are the times when I have the most leeway to factor in other considerations. I will consider the probabilities to be close when the gap is less than an eighth of their value. (Note that this is a different and more correct scheme than the one I used to distinguish which probabilities were close in my previous article.) The probability is close for these hands:

Two lands in a seven-card hand.
Five lands in a six-card hand.
Zero, one, and five lands in a five-card hand.
Any four-card hand.

These guidelines differ only very slightly from the guidelines found on the draw.

For six-card hands with five lands, the guidelines say to mulligan on the play and keep on the draw.
For five-card hands with one land, the guidelines say to mulligan on the play and keep on the draw.

As expected, the guidelines call for more mulligans on the play, but not dramatically more.

Mana Development on the Play

The mulligan guidelines give me a mathematical model for how mulligans affect starting hands. I can now account for mulligans in my calculations and get a more accurate picture of mana development. Since I now have mulligan guidelines both on the play and on the draw, I can compare how mana develops differently between the two players.

One thing of particular interest is how long the speed advantage persists when I am on the play. When I’m on the play, I’m the first to play a land. My opponent gets an extra card. I get a huge head start on mana development, but in the long run the extra card should win out. At some point my opponent’s mana development should outstrip mine, if only slightly. Is that true, and on what turn does it generally occur? I will answer that question before the end of this section.

Lands in Play

In a previous article, I calculated the average number of lands I have in play on a given turn. In that calculation, I assumed a three-land starting hand. I can now account for mulligans and no longer have to make such assumptions. Previously I averaged games on the play and draw. Here I keep the results separate.

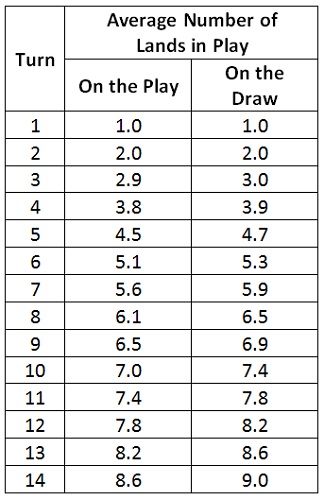
During the early and midgame, the land counts leapfrog, with the player whose turn it is having the highest average land count. The first player has the highest land count during their turn because they get to go first. The second player has the highest land count during their turn because they have access to more cards and are more likely to have a land in hand to play.

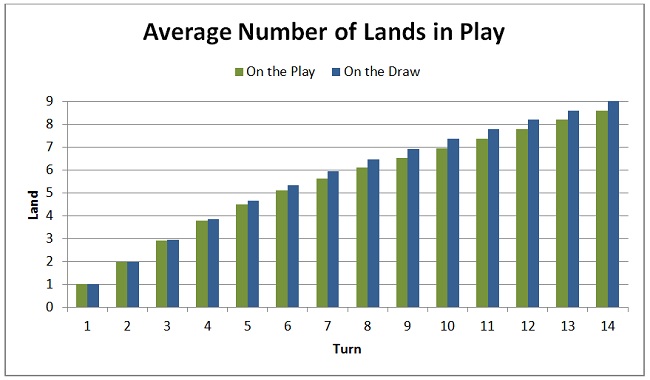
That remains true up until around turn 11 or 12, at which point the player on the draw pulls ahead. From that point on, the average land count of the player on the draw is equal or greater than their opponent’s average count on their next turn. In other words, the second player has the higher average land count from then on.

Land Count Difference

I can look at the difference in average land counts by subtracting the first player’s average from the second player’s.

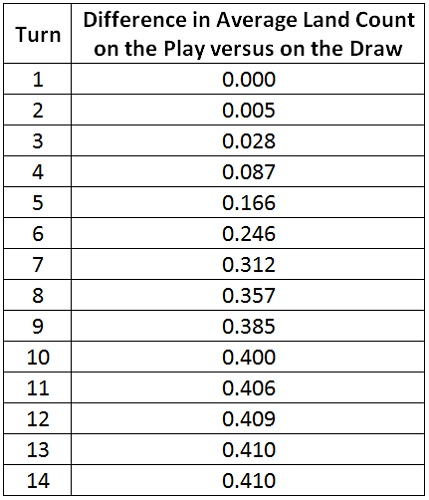
The difference grows asymptotically towards 0.410. A graph makes the numbers more clear.

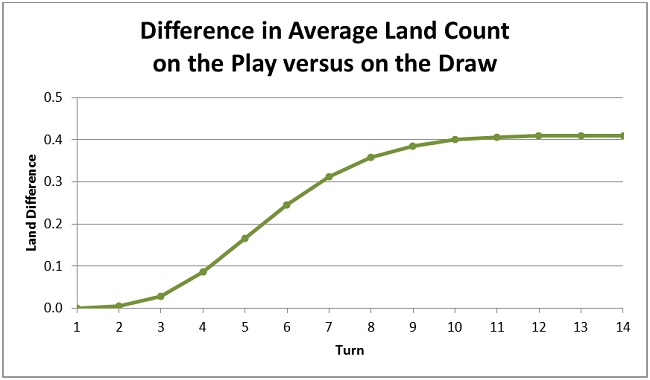
I honestly had expected the late game difference in land count to be 0.425, not 0.410. The percent of my deck that is land is 42.5%. That’s 17 over 40. So I had thought that the second player’s one extra card would correspond to 0.425 more lands on average.

Why 0.410? After some thought, it makes perfect sense. Before I draw my opening hand, the percentage of land in my library is 42.5%. However, after the application of mulligans, my library’s average land percentage is reduced. The use of mulligans pulls a greater than expected number of lands into my opening hand, and a smaller than expected amount ends up in my library. What is the average percent of my library that is land after mulligans? I can calculate that.

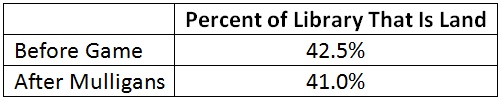
There you go. That accounts for the second player’s 0.410 land count lead in the late game.

Mana Growth Rate

I can also compare the rate of mana growth between the two players by subtracting the average land count on each turn from the previous turn’s count.

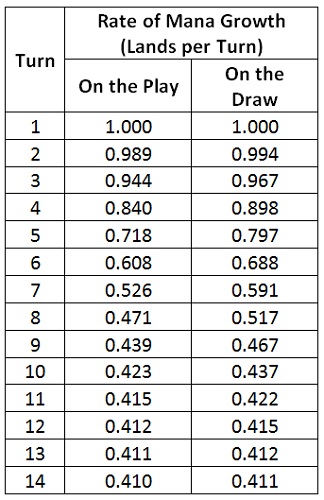
Early in the game the players have similar and strong mana growth rates. During the mid game the growth rates drop, but the second player’s rate does not fall as quickly. This is when the second player pulls ahead in the average land count. In the late game the players’ growth rates again becomes similar, settling at 0.410.

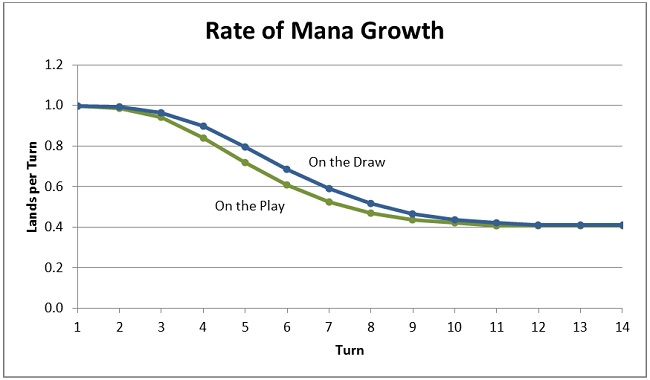
Here we see the number 0.410 again and for the same reason. It is the percent of my library that is land after mulligans, and thus it is the rate at which I can expect to draw land.

First to a Land Count

Which player is more likely to get to a particular land count first? That is something I can calculate. Across all games played, in what percentage will the first player reach that land count before the second player?

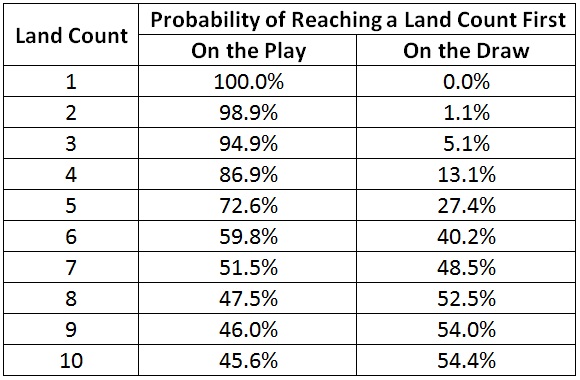
As you’d expect, for low land counts the first player’s percentage is very high. The first player almost always reaches low land counts first. The only time they won’t is when they have an extremely poor starting hand, and the probability of that is low.

As we look at higher land counts, the first player’s probability of reaching each land count first drops steadily. By the seventh land, the starting player’s speed advantage has dwindled to almost nothing. The eighth land is the first land that the player on the draw has a greater-than-even chance of playing first. The second player’s card advantage has overtaken the first player’s speed advantage.

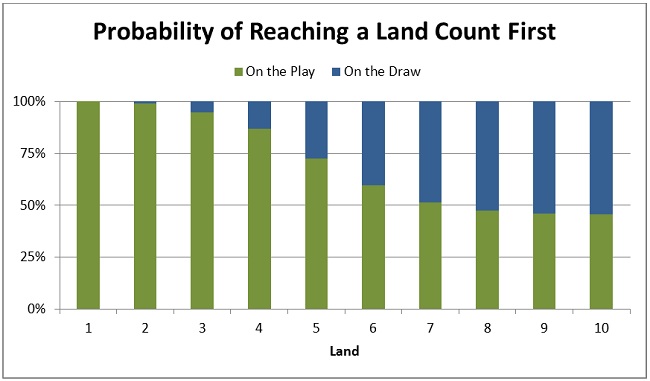
The first player’s speed advantage lasts, on average, until the seventh land. Looking back at the earlier table that lists the average land count on each turn, I can see that the seventh land is generally played around turn 10. So when I am on the play, my speed advantage, at least with respect to mana development, lasts until about turn 10. That is very late in the game! No wonder everyone chooses to play first.

Different Decks

Before ending my discussion of mulligans, I want to look at two different decks that warrant different mulligan guidelines.

For the following calculations, I do not include all of the numbers and tables. It would simply be too much. If you are curious to see the details of the math, download the Magic Probability Toolkit. I now include in the download the output of all calculations used in my articles. Compiling and running the code is no longer required. The data is included in both a human-readable text file as well as a CSV file that can be opened in Excel.

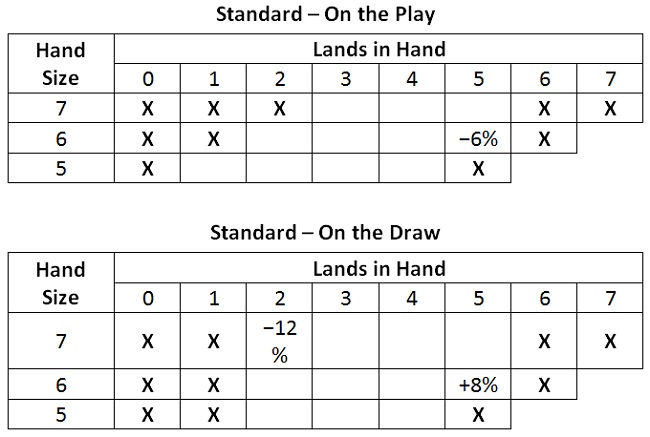
Each set of mulligan guidelines is presented as a table. Entries with an ‘X‘ mean mulligan. Entries that are blank mean keep. Entries with a number mean that the probability gap between mulling and keeping is small, within an eighth of their value. In that case, other factors should also be considered when making the mulligan decision.

The percentage listed is the difference between the probability of obtaining a competitive start by keeping and by mulling. A positive percentage means the math favors a keep. A negative percentage means the math favors a mulligan. The farther the percentage is from zero, the more strongly the math favors the indicated action. (For example if negative 12% is listed, that means a mulligan gives a 12% higher relative probability for obtaining a competitive start than keeping.)

Standard Competitive Start

I’ll start with the mulligan table for the guidelines derived in this and the previous article. They use the standard definition of a competitive start: four lands and four spells by turn four.

High Land-Count Decks

Here are the mulligan guidelines appropriate for a deck with nineteen lands instead of seventeen. I have left the definition of a competitive start unchanged.

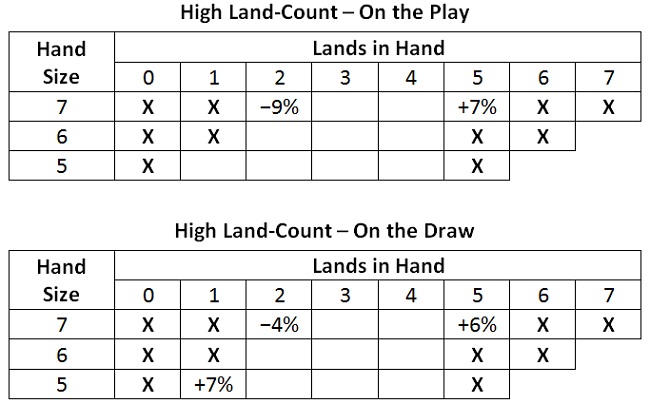
The higher land count in a nineteen-land deck allows for much more aggressive mulligan behavior. Hands with a low land count are rarer, so you are taking less of a risk when you mulligan.

Low-Curve Decks

Sometimes a Limited format supports a very aggressive deck with an extremely low mana curve. Such a deck can win quickly and do so using only three mana. In particular, I am thinking of the R/W and R/G Avacyn Restored decks. You can also build a Rakdos deck that plays like that, but the powerful and aggressive four- and five-drops in Rakdos often pull you into a deck with more staying power and a larger appetite for mana.

In any case, such decks benefit from a different mulligan goal. They require more gas and less mana.

Three lands by turn 4.
Five spells by turn 4.

Changing the definition of a competitive start will cause the math to lead us to different mulligan guidelines. Here are the mulligan guidelines that result.

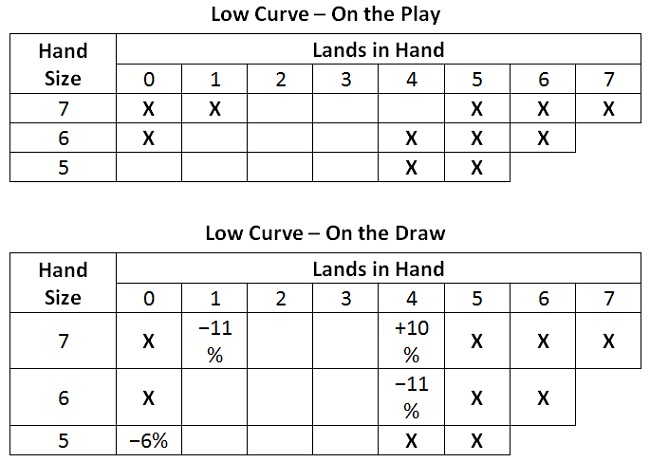
Not surprisingly, this goal results in guidelines with a window of keeping that is shifted to the left by about one land.

Takeaways

The chance of missing your third-turn land drop when you start with a two-land hand is 15% on the draw and 30% on the play.

The starting player’s speed advantage, at least with respect to mana development, lasts until about turn 10.

See the charts above labeled Standard – On the Play and Standard – On the Draw for the mulligan guidelines derived in this article.

[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit