Everyone hates to mulligan, myself included. People look for any excuse not to, especially new players. After someone draws a hand flooded with land, it’s not uncommon to hear:
Is there any truth to that? Does the chance of drawing spells really go up when my hand is flooded with land? Let’s apply some mathematics and find out.
To use math, I need to boil things down to a specific question: if I keep a six-land hand, how much does that change my chance of drawing a land first turn?
First I need to figure out the chance for a normal hand. Then I can compare it to a flooded hand. I’ll say a normal hand is seven cards with three lands. If I’m playing a standard Limited deck of 40 cards with seventeen lands, after I draw my starting hand there are 33 cards left in the library, of which 14 are lands. The chance of drawing land on my first turn is fourteen in 33, or 42.4%.
The flooded hand has six lands in it, which leaves only 11 in the library. So the chance of drawing a land is eleven in 33, or 33.3%. Here are the probabilities in a table.
| Lands in Starting Hand | Probability of Drawing a Land First Turn |
| 3 | 42.4% |
| 6 | 33.3% |
Looking at the numbers, I see that the chance of drawing a land first turn when I’m flooded goes down by about 9%. That isn’t very much. A 9% difference means my draw will only be affected by the fact that I am flooded in one out of every 11 games. Most games, the flooding will make no difference at all.
With a six-land hand my first turn draw is going to be a land 33% of the time, or one out of every three games. I’ve heard players complain about their luck when they keep a flooded hand and then draw into more land. Now I know they have no right to complain. Hitting a one in three chance isn’t unlucky. It’s just a bad bet.
Land Flood
Let’s look beyond the first card drawn. If I plan to survive the early game with a six-land hand, I need to draw a strong run of spells. The first draw doesn’t necessarily need to be a spell, but I definitely want spells to be the majority of my early draws. So here’s a question worth answering: what is the chance that at least three of the first four cards I draw are spells?
This isn’t the sort of calculation I can do on the back of an envelope, so I’ll use my Magic Probability Toolkit (available here) to crunch the numbers. The technique is exactly the same as the one I demonstrated in my previous article. (I list every possible set of draws that can occur. Then I calculate the probability of each scenario. Finally I sum the probability of any scenarios that give the same answer to the question I’m trying to answer.)
For fun, I didn’t just do the calculation for a six-land starting hand. I also did the calculation for land counts two through seven. Here are the results I got.
| Lands in Starting Hand | Probability of At Least Three Spells in the First Four Draws |
| 2 | 37.4% |
| 3 | 42.6% |
| 4 | 48.1% |
| 5 | 53.6% |
| 6 | 59.3% |
| 7 | 64.9% |
Here’s the same data as a graph.

From the graph I can see that the probability increases with the number of lands I have in my starting hand. That’s good news since the fewer spells I have, the more important it is for me draw some. A three-land hand gives me a 43% chance of drawing three or more spells, while a six-land hand gives me a 59% chance. That’s up 16%.
However, a 16% increase is not large enough to make my six-land hand acceptable. If I have a 59% chance of drawing three or more spells, that means I have a 41% chance of drawing less than three spells. I have a 41% chance of drawing zero, one, or two spells. At best that leaves me with eight lands and three spells on turn 4. That’s a horrible situation to be in. Keeping a six-land hand means a 41% chance of flooding out completely in the early game.
Card Advantage
Let’s suppose I survive the early game. How does a six-land hand affect my mid to late game?
When I draw an excessive number of lands, my opponent is effectively gaining card advantage. They’re getting impactful cards while I’m drawing blank cardboard. From a game design perspective, this does great things for Magic. It adds variance to both the early and late game. You never know who’s going to get more gas or when they’ll get it. Even a really bad player can occasionally beat the world’s best if the better player just draws too much land.
While variance is good for the game as a whole, it can be a disaster when I’m trying to win. I absolutely do not want my opponent to have a card advantage, and that’s effectively what they start with when I keep a six-land hand.
However, the start of the game is not when card advantage has its greatest impact. Card advantage is most important in the mid to late game, when hands begin to empty out. One player runs out of gas, while the other continues to drop creatures and sling removal.
When I keep a six-land hand, how much effective card advantage is my opponent likely to have once we reach the mid game?
For this calculation, I assume that my opponent starts with a three-land hand and I start with a six-land hand. I calculate how many more spells my opponent has at the end of the seventh turn. I perform the calculation twice, once with me going first and once with my opponent going first. Then I average the results.
I’m going to use the term “spell advantage” to refer to an effective card advantage caused by land flood. My opponent’s spell advantage is the number of spells he has access to minus the number of spells I have access to.
Here are my findings.
| Lands in Starting Hand | Average Spell Advantage of Opponent Mid Game |
| 2 | -0.8 |
| 3 | 0.0 |
| 4 | 0.8 |
| 5 | 1.6 |
| 6 | 2.4 |
| 7 | 3.2 |
If I keep a six-land hand, my opponent will have, on average, about two-and-a-half more spells at the mid game.
I’d naively expect my opponent to average a three-spell advantage when I keep a six-land starting hand since I start the game with three fewer spells. However, the fact that I have more lands in my hand and thus less in my library means I’m slightly more likely to draw spells than my opponent. That helps me catch up.
It’s interesting to note that this effect is more pronounced due to the small size of Limited decks. If we were playing 60-card Constructed decks, the average advantage would rise to 2.6 spells. Playing 100-card Commander decks, the advantage is 2.8 spells. Here is another reason, albeit a minor one, to limit your deck to 40 cards: it helps smooth out your land draws.
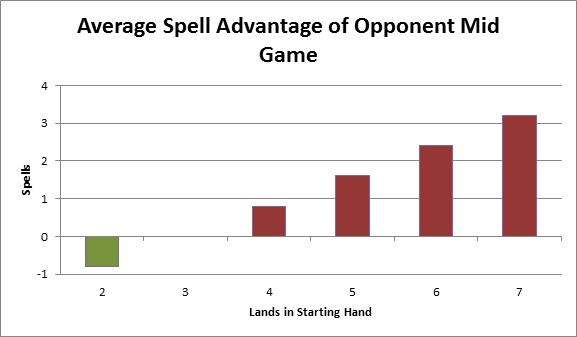
I want to glance at a few other numbers in the table as well. The negative number for a two-land hand means that I am the one with the spell advantage, not my opponent. That’s because in this case I’m starting the game with one more spell than my opponent. It’s basically the opposite of the four-land hand.
The average advantage comes out as zero for a three-land hand. That makes sense because I’m starting with the same number of spells as my opponent. Averaged over all games, neither of us should have an advantage.
Escaping the Advantage
It’s hardly surprising that the average case with a six-land hand is that I’m behind on spells. However, there’s always some chance I could escape that fate. There’s some probability that I’ll draw plenty of spells, my opponent will draw nothing but land, and I’ll crawl out of my spell disadvantage by the mid game.
What is the chance I crawl out of that hole? What is the probability my opponent’s spell advantage disappears by the mid game?
Using the same suppositions as the previous calculation, here are my results.
| Lands in Starting Hand | Probability of Opponent Having No Spell Advantage Mid Game |
| 2 | 77.6% |
| 3 | 61.4% |
| 4 | 43.1% |
| 5 | 25.9% |
| 6 | 12.9% |
| 7 | 5.1% |
The probability of crawling out of my spell disadvantage hole when I keep a six-land hand is 13%. That’s very low. Correspondingly, the probability of my opponent retaining their spell advantage through to the mid game is opposite that, or 87%. Six-land hands are not so hot.
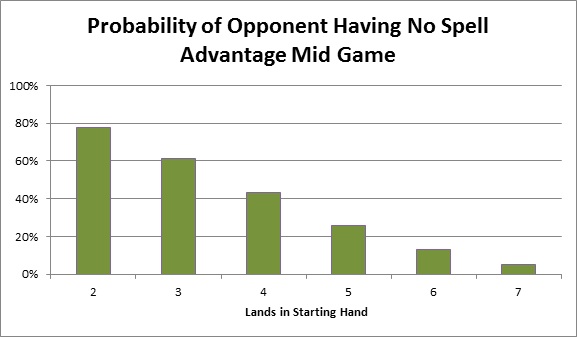
Here’s a question that could be asked about these results: why is the probability not 50% for a three-land starting hand? After all, I’m assuming my opponent starts with three lands, so in that case we both start with equal spell counts. Why is the probability higher than 50%? The reason is that this probability includes the cases in which my opponent and I have equal spell counts.
The possibilities break down like this. My opponent has a 39% chance of having a spell advantage. I have a 39% chance of having a spell advantage. Those chances are equal because we start with the same number of spells. Finally, there is a 22% chance that we have equal spell counts at the mid game. If we have equal spell counts, my opponent does not have a spell advantage. So the total probability of my opponent not having a spell advantage is 39% plus 22%, or the 61% shown in the table.
Takeaways
Don’t keep a six-land hand. There’s about a 40% chance you’ll flood out completely. If you survive the early game, you should expect your opponent to have about a two-and-a-half spell advantage over you in the mid game. Mulligan!
[email protected]
@DanRLN on Twitter
source code for the Magic Probability Toolkit
 |
I’m with the Simic Combine. I’m a scientist, but I’m also a lover of nature. Plus, enemy color combinations always produce more interesting spells, and of all enemy colors, blue-green has the smallest overlap in both abilities and flavor. So blue-green cards are always crazy awesome! I mean, come on. Mystic Snake! |
